thomas
deckker
architect
critical reflections

Vaux-le-Vicomte: Architecture and Astronomy
2022
2022

Louis Le Vaux and André Le Nôtre: Vaux-le-Vicomte, Entrance Court
engraving by Israel Sylvestre
engraving by Israel Sylvestre
Vaux-le-Vicomte: Architecture and Astronomy
This article is an edited version of an article prepared for publication on landscape architecture in France in the 17th century, and of the links between architecture, mathematics and astronomy. The first article on Architecture and Astronomy was on The Temple of Apollo at Stourhead.
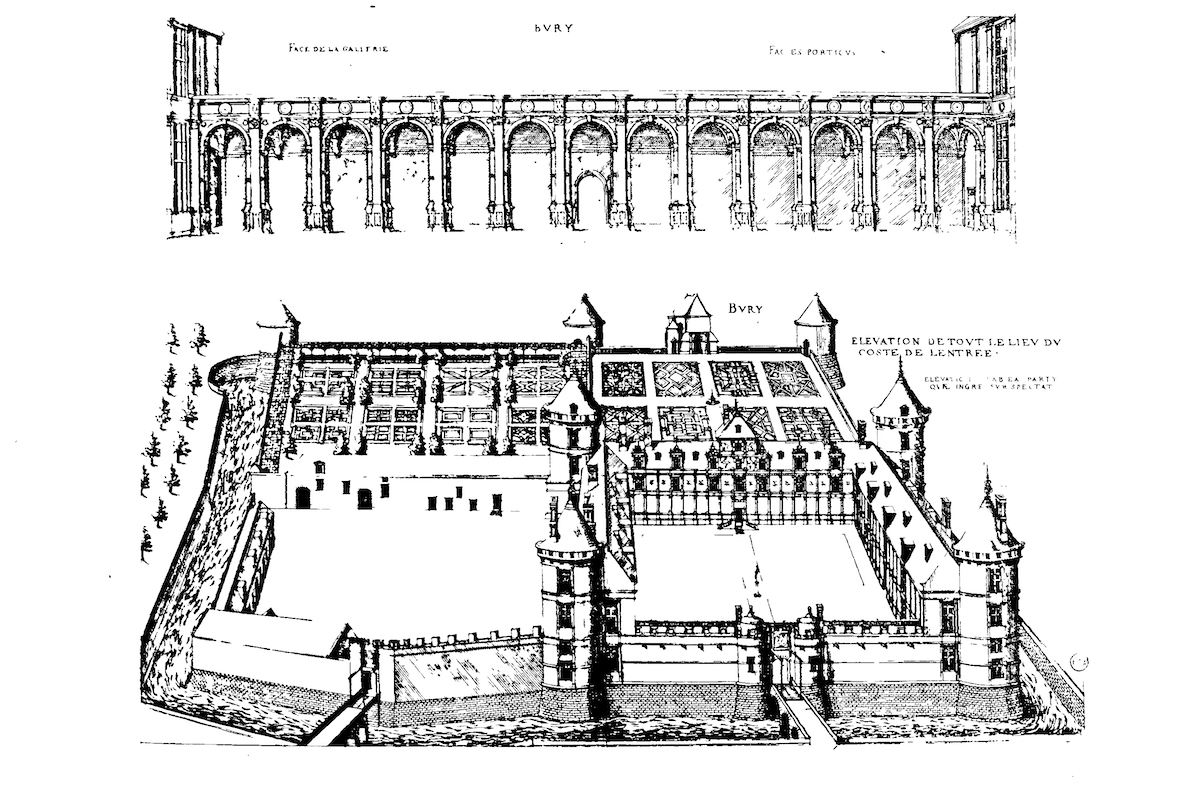
Chateau de Bury
Jacques Androuet du Cerceau: Les plus excellents Bastiments de France (Paris 1576/79)
Jacques Androuet du Cerceau: Les plus excellents Bastiments de France (Paris 1576/79)

Jardin de Diane de Poitiers, Château de Chenonceau
© Thomas Deckker 1984
© Thomas Deckker 1984
In the middle of the 17th century there was a major change in the design of landscapes in France. The extent of this change may be seen in comparison to earlier ensembles of house and garden: French Renaissance gardens usually had formal jardins - rectangular and enclosed, such as the first at the Château de Bury (1511-24) and the Château de Chenonceau (1515-) in the Loire, which were illustrated by Jacques Androuet du Cerceau in Les plus excellents bastiments de France in 1579.

Louis Le Vaux and André Le Nôtre: Château de Vaux-le-Vicomte, view of the gardens
engraving by Israel Sylvestre
engraving by Israel Sylvestre
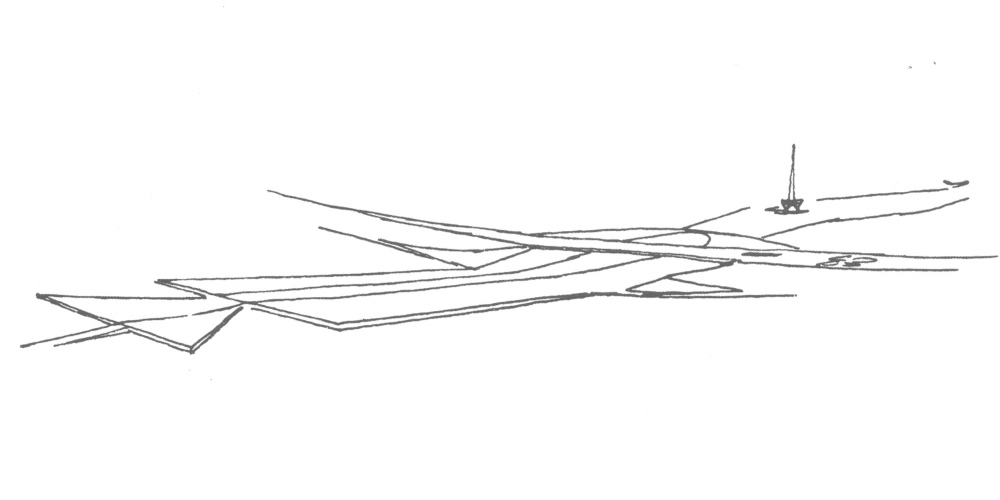
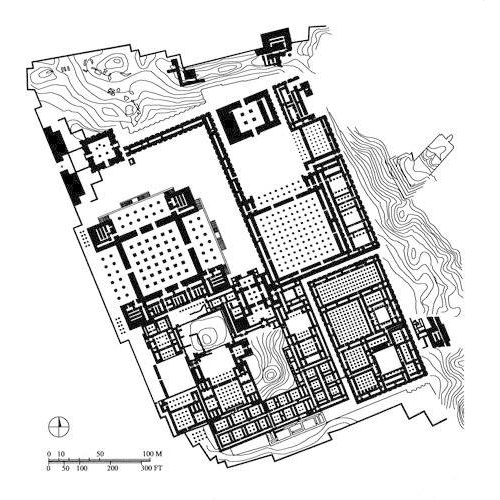
The Château de Vaux-le-Vicomte (1657-61), designed for Nicolas Fouquet by Louis Le Vau with gardens by André Le Nôtre, was the first of what became known as baroque landscapes. Vaux-le-Vicomte has an axial sequence from entrance court to a colossal forest landscape extending several miles towards the horizon. By clever use of the rising ground to the south Le Nôtre gave the illusion of the woodlands stretching to infinity. The view through the windows of the oval salon mirror the allées in the pâte-d'oie sweep out landscape space.
These sweeps of landscape space in turn mirror the new concept of elliptical planetary orbits put forward by Johannes Kepler in 1609. The implication is clear: whoever stands in the salon lies at the focus of a universe, whose extension into infinite space is embodied in the allées. Leonardo Benevelo, in Architecture of the Renaissance (London: Routledge and Kegan Paul 1978) noted that:
These sweeps of landscape space in turn mirror the new concept of elliptical planetary orbits put forward by Johannes Kepler in 1609. The implication is clear: whoever stands in the salon lies at the focus of a universe, whose extension into infinite space is embodied in the allées. Leonardo Benevelo, in Architecture of the Renaissance (London: Routledge and Kegan Paul 1978) noted that:
Le Nôtre's aim was… to attempt the physical representation of the infinite, rather than the figurative representation; in other words, to control a whole portion of the countryside, from foreground to background, according to the criteria of regularity and symmetry. He used avenues, flowerbeds, terraces, pools and fountains to this end, but organized them in a calculated system which interpreted the geographical situation of the place, and aimed at the total rationalization of the landscape, including the background at infinity.
Louis XIV, the Sun-King, took exception to Fouquet's presumption at the opening party, confiscated the château and imprisoned Fouquet for life.
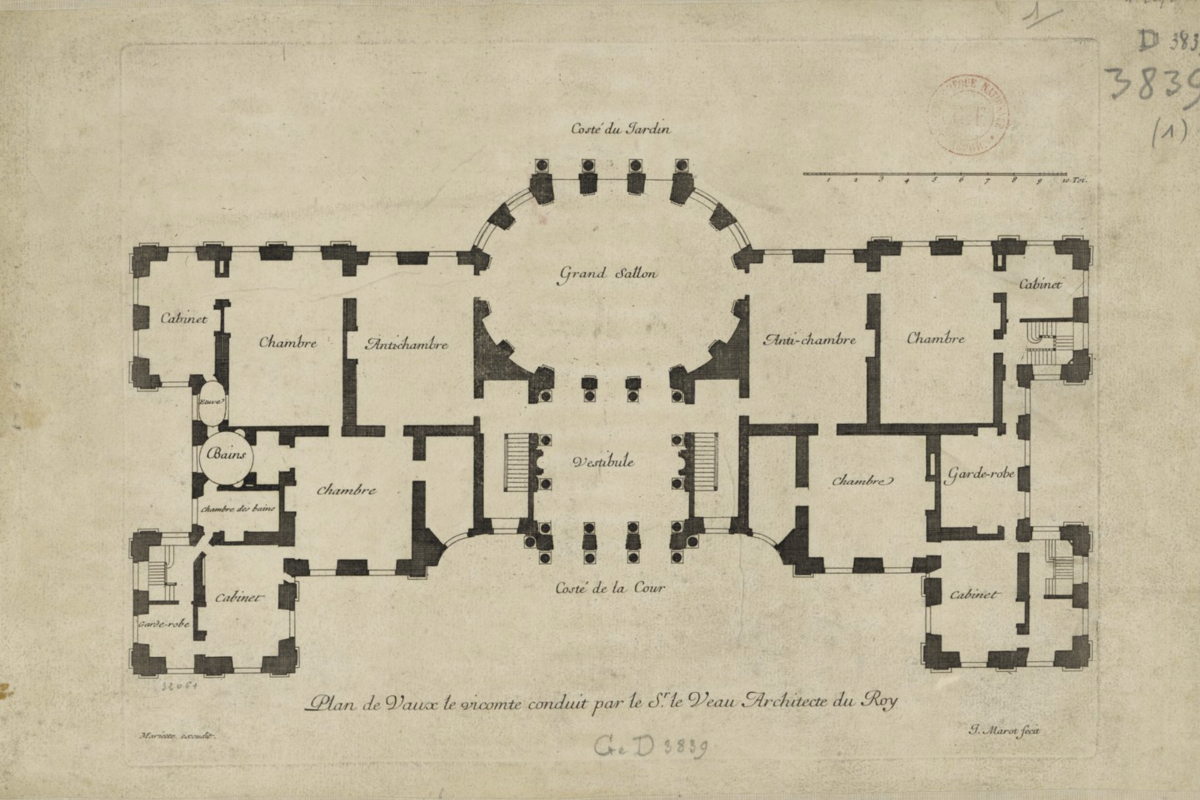
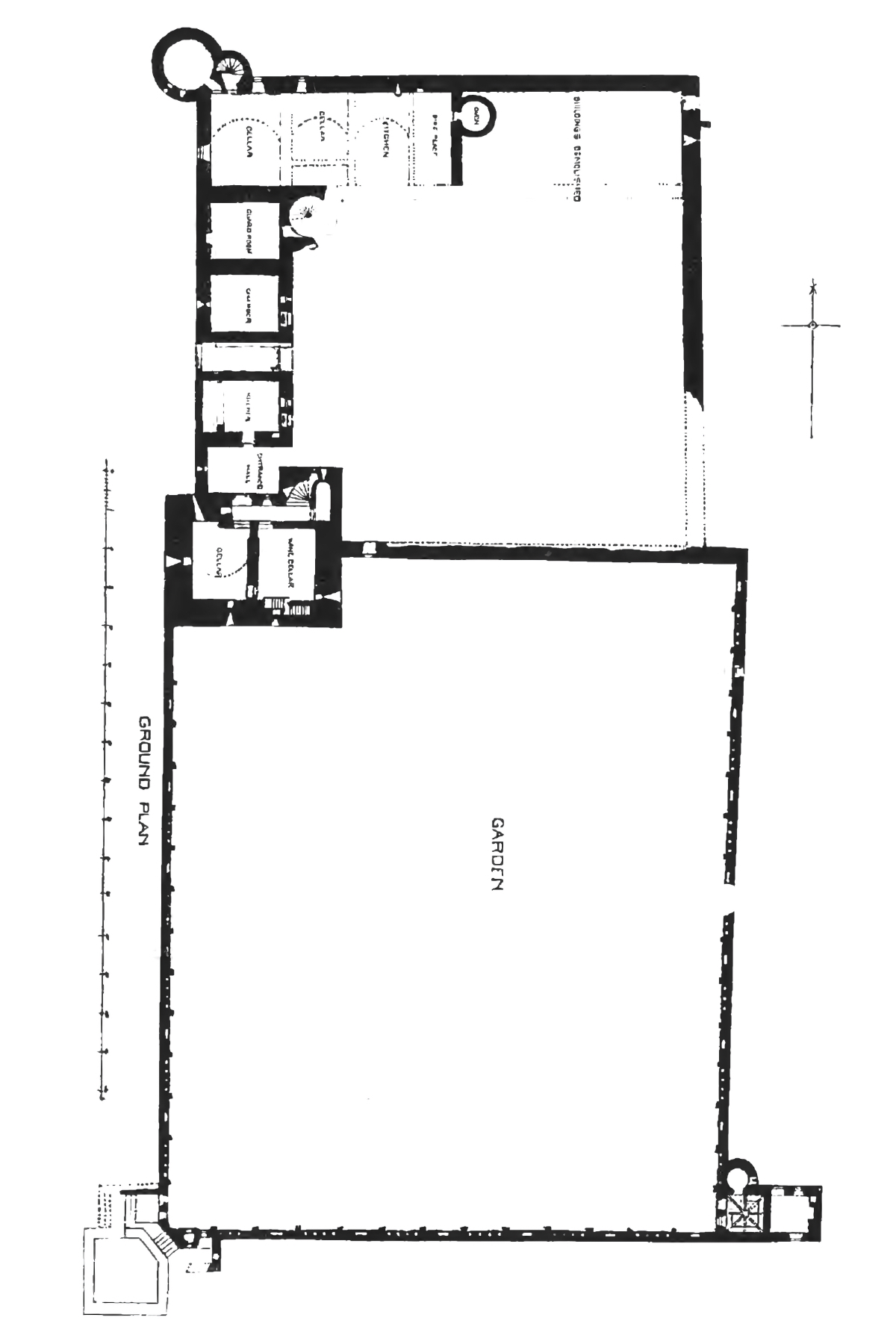
Louis Le Vaux: Vaux-le-Vicomte
Engraving of ground floor plan by Jean Marot
Engraving of ground floor plan by Jean Marot
roll over for illustration of sweeps of space
While we now think of music, astronomy, mathematics and architecture as distinct disciplines, in the 16th century they were all seen as expressions of divine harmony. They shared a common basis in Euclidean geometry - that is, geometric space that could be visualised in two or three dimensions, and the Platonic solids - solid shapes made from identical faces that conjured up particular ratios. Mathematics, geometry, music, and astronomy formed the quadrivium, the basis of education in the arts, and thus concepts could easily cross the boundaries of disciplines. Claude Perrault, for example, a founder of the Académie Royale des Sciences in 1666, was a physician and musical theorist as well as architect of the East Wing of the Louvre (1667-70). Christopher Wren, a founder of The Royal Society in 1660, had been Savilian Professor of Astronomy at Oxford University before being appointed Surveyor of the King's Works in 1669 and thus architect of St Paul's Cathedral (1670-1698). These connections have been studied by George L. Hersey in Architecture, Poetry and Number in the Royal Palace at Caserta (MIT 1983) and Architecture and geometry in the age of the Baroque (University of Chicago Press, 2000) and Anthony Gerbino and Stephen Johnston in Compass and Rule: Architecture as Mathematical Practice in England 1500-1750 (Yale University Press 2009).

Johann Kepler: model of the solar system after Copernicus
Kepler initially proposed that the planets occupied fixed orbits in ratios according to the Platonic solids, based on Copernicus's theory that the earth revolved around the sun. This was published before Kepler's work on conic sections, which introduced him to the mathematics of ellipses.
Johann Kepler: Mysterium cosmo-graphicum (Tübingen, 1596)
Kepler initially proposed that the planets occupied fixed orbits in ratios according to the Platonic solids, based on Copernicus's theory that the earth revolved around the sun. This was published before Kepler's work on conic sections, which introduced him to the mathematics of ellipses.
Johann Kepler: Mysterium cosmo-graphicum (Tübingen, 1596)

Johann Kepler: conic sections
Kepler's treatise on conic sections was a commentary on Perspectiva [Optics], written by the Polish scientist Witelo c. 1280 and published in Basel in 1572. The page shows a circle, ellipse, parabola and hyperbola, all sections of a cone, hence conic sections.
Johann Kepler: Ad Vitellionem Paralipomena (Frankfurt 1604)
Kepler's treatise on conic sections was a commentary on Perspectiva [Optics], written by the Polish scientist Witelo c. 1280 and published in Basel in 1572. The page shows a circle, ellipse, parabola and hyperbola, all sections of a cone, hence conic sections.
Johann Kepler: Ad Vitellionem Paralipomena (Frankfurt 1604)

Johann Kepler: the first 2 laws of planetary motion
After writing his treatise on conic sections, Kepler proposed the first 2 of his 3 laws of planetary motion: that the orbits of the planets were ellipses with the sun at one focus, and that the speed along this orbit was proportional to the area of the sweep of space between the planet and the sun.
Johann Kepler: Astronomia nova (Prague 1609)
After writing his treatise on conic sections, Kepler proposed the first 2 of his 3 laws of planetary motion: that the orbits of the planets were ellipses with the sun at one focus, and that the speed along this orbit was proportional to the area of the sweep of space between the planet and the sun.
Johann Kepler: Astronomia nova (Prague 1609)
The breakthrough that the earth revolved around the sun was made by Nicolas Copernicus in De revolutionibus orbium coelestium in 1543, but he could not explain the motion of the planets whose orbits could be more carefully observed through the newly-founded telescopes. The further breakthrough, that the orbits were ellipses, was made by Kepler. Kepler's conjecture gave a convincing structure to the Heavens in computable mathematics, which, like the optics of the telescopes used to observe the motion of the planets, was based on the newly-rediscovered conic sections. Furthermore, it broke the notion that the orbits were in fixed definable ratios and introduced the idea of infinity. Kepler illustrated the ellipitical orbits with rays extending from the focal points.
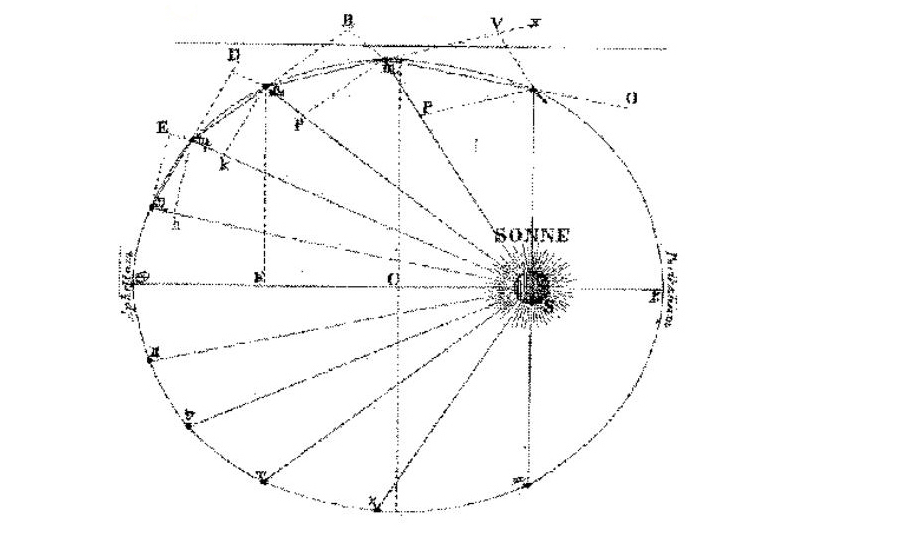
Johannes Kepler: Planetary Elliptical Orbit (redrawn in the 19th century)
Kepler's Three Laws of Planetary Motion were based entirely on the sweeps of space from the sun, one focus of an elliptical orbit of a planet. The orbit of a planet was, literally, defined by the sweeps, which look remarkably like the pâte-d'oie of Le Nôtre.
roll over for illustration of sweeps of space
Conic sections - ellipses, parabolas and hyperbolas - represented a major change in the understanding and use of mathematical shapes. Conic sections could not be derived from simple mathematical formulae: they were derivative of projections of one shape onto another, such as a plane and a cone. Kepler had published a treatise on conic sections in his work on optics in 1604 and it was this study which certainly provided the conceptual breakthrough for his treatise on elliptical orbits in 1609.

Ismael Boulliau: astronomia philolaica
A treatise circulating in Paris at the middle of the 17th century. Boulliau refined Kepler's mathematics relating to ellipses.
Ismael Boulliau: astronomia philolaica (Paris 1645). One of several diagrams illustrating Kepler's conjecture on elliptical orbits, in particular with rays sweeping out space from the focal points.
Ismael Boulliau: astronomia philolaica (Paris 1645)
A treatise circulating in Paris at the middle of the 17th century. Boulliau refined Kepler's mathematics relating to ellipses.
Ismael Boulliau: astronomia philolaica (Paris 1645). One of several diagrams illustrating Kepler's conjecture on elliptical orbits, in particular with rays sweeping out space from the focal points.
Ismael Boulliau: astronomia philolaica (Paris 1645)
Treatises on descriptive geometry - representing three-dimensional objects in two dimensions, projective geometry - the science of perspective, and conics were circulating in France among architects in the early 17th century. The mathematician Ismael Boulliau, a member of the Académie, developed Kepler's conjectures further mathematically. Girard Desargues, considered by mathematicians to be one of the founder of projective geometry, was important enough as an architect for his design for the hôtel Roland (c. 1648) in Paris to be illustrated in two major catalogues of French architecture, the Petit Marot in 1654 and the Grand Marot in 1670. The connection was practical as well as intellectual: the invention of the new optical instruments had practical uses in measuring and setting out buildings and landscapes; the theodolite and level were made more accurate by the use of the telescope for sighting long distances and microscope for reading vernier scales. As Maurice Daumas noted, in Scientific instruments of the seventeenth and eighteenth centuries and their makers (London: Batsford, 1972), the astronomer Jean Picard, another member of the Académie, famous at the time for accurately measuring the diameter of the Earth, made a telescopic level for setting out the gardens at Versailles, necessary because of the large basins of water and poor water supply.
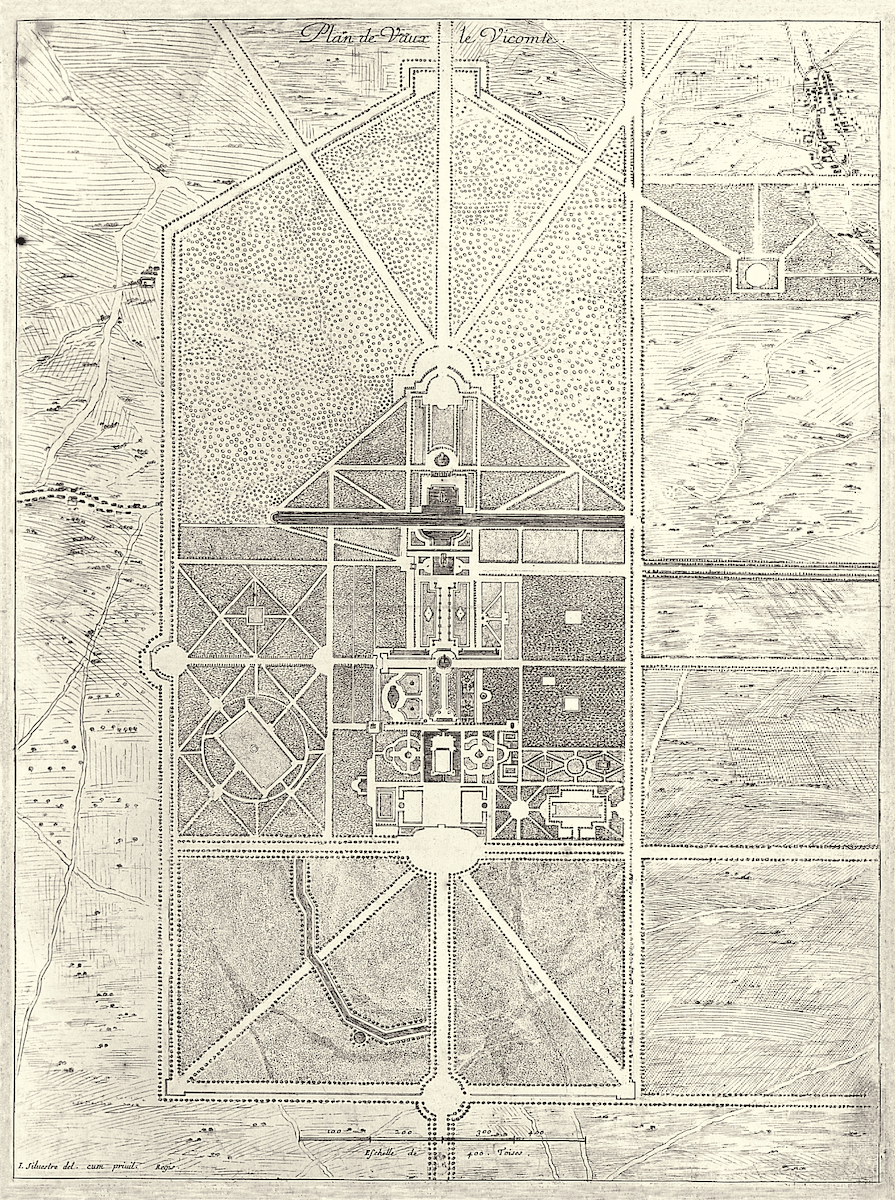
Louis Le Vaux and André Le Nôtre: Château de Vaux-le-Vicomte, site plan
roll over for illustration of sweeps of space
The ellipse, unthinkable in architecture in the early renaissance (as it was not a Platonic solid), became design currency during the 16th century when translations of 2 important treatises on conic sections from Antiquity - Synagoge by Pappus of Alexandria and Conics by Apollonius of Perga - had been printed. The Campidoglio (1546) by Michelangelo and Sant'Andrea in Via Flaminia, the first elliptically-domed church (1554), by Vignola - to its full flowering among Roman architects in the 17th century: San Carlo alle Quattro Fontane (1634-46) by Borromini, and the Piazza San Pietro (1656-1667) by Bernini. Not only were these buildings known through treatises in France, but Bernini himself was in Paris in 1665, at the invitation of Louis XIV, to design the new East Wing of the Louvre, although the commission went to Claude Perrault instead. The Piedmontese architect Guarino Guarini was also in Paris between 1662 and 1666, working on the church for his Theatine order in the newly-urbanised Faubourg Saint-Germain. The oval salon at Vaux-le-Vicomte would not be such an innovation if it was not clearly part of a larger scheme of landscape space.
It is likely that Louis XIV imprisoned Fouquet not because of his extravagance, as is commonly supposed, but because he recognised that Vaux-le-Vicomte was a literal representation of the sun as the centre of an infinite universe. This was a position he reserved for himself: he took Le Vau and Le Nôtre to Versailes, where he built the same but bigger and, perhaps, a little less interesting.
Thomas Deckker
London 2022
London 2022